数据在计算机系统内形成、存取和传送过程中,可能会因为某种原因而产生错误,如将0误传为1等。为减少和避免这类错误,一方面需要从电路、电源、布线等硬件方面采取措施,提高计算机硬件本身的抗干扰能力和可靠性;另一方面可以在数据编码上采取检错纠错的措施,即采用某种编码方法,使得机器能够发现、定位乃至纠正错误。
具有检测某些错误或带有自动纠正错误能力的数据编码称为数据校验码。数据校验码的实现原理是在正常编码中加入一些冗余位,即在正常编码组中加入一些非法编码,当合法数据编码出现某些错误时,就成为非法编码,因此就可以通过检测编码是否合法来达到自动发现、定位乃至改正错误的目的。在数据校验码的设计中,需要根据编码的码距合理地安排非法编码的数量和编码规则。
错误纠正编码的现代发展在1947年由理查德·卫斯里·汉明带来,即海明码/汉明码。
海明距离:一组编码中任何两个编码之间代码不同的位数,换句话说,就是将一个编码变换成另外一个编码所需要替换的字符个数。(在信息论中,两个等长字符串之间的汉明距离(英语:Hamming distance)是两个字符串对应位置的不同字符的个数。换句话说,它就是将一个字符串变换成另外一个字符串所需要替换的字符个数。 ————维基百科)
码距:在一组编码中任何两个编码之间最小的距离
例如编码0011与0001,仅有一位不同,称其海明距离为1。如果采用四位二进制编码表示16种状态,因为从0000到1111这16种编码都用到了,所以这组编码的码距为1。也就是说,在这组编码中任何一个状态的四位码中的一位几位出错,都会变成另一个合法编码,所以这组编码没有查错和纠错能力。但是,如果采用四位二进制表示8个状态,例如只将其中的8种编码0000、0011、0101、0110、1001、1010、1100、1111用作合法编码,而将另外8种编码作为非法编码,此时这组编码的码距为2,即从一个合法编码改为另一个合法编码需要修改2位。如果在数据传输过程中,任何一个合法编码有一位发生了错误,就会出现非法编码。例如编码0000的任意一位发生错形成的编码都不是合法编码,因此系统只要检查编码的合法性,就可以发现错误。
校验码通常是在正常编码的基础上按特别规定增加一些附加的校验位形成的,即通过增大编码的码距来实现检查和纠正错误的目的。一般来说,合理地增加校验位、增大码距,就能提高校验码发现错误的能力。如上所述,要检查1位错误,编码的码距需要1+1=2。而要检查e位错,编码的码距需要e+1,因为对于这样的编码,一个码字e位出错就无法将一个合法编码变为另外一个合法编码。类似地,如果出错的位置能够确定,将出错位的内容取反,就能够自动纠正错误。而要纠正t位错,编码的码距需要2t+1。这是因为当码距达到2t+1时,即使合法编码中有t位出错,它与原合法编码的编码距离还是比与其他任何合法码字的编码距离要小,这样就可以惟一地确定它的合法编码,即可以自动纠正错误。
例如,考虑下面只有四个合法编码0000000000、0000011111、1111100000、1111111111的编码组。可以看出这个编码组的码距为5,意味着它能纠两位错。如果在数据传输过程中,接收方接收到一个编码0000000111,就能够知道原来的正确编码应0000011111(必须假定不出现两位以上的错误)。当然,如果错了3位,即0000000000变成了0000000111就无法确定0000000000出现了错误,还0000011111出现错误,因而无法纠正错误,即码距为5时,只能够纠两位错
由此可见校验位越多,码距越大,编码的检错和纠错能力越强。设码距为d,码距与校验码的检错和纠错能力的关系是:
d≥e+1,可检验e个错
d≥2t+1,可纠正t个错
d≥e+t+1,且e>t,可检验e个错并能纠正t个错

由于数据校验码所使用的二进制位数比常数据编码要多,所以在使用过程中,将增加数据存储的容量或数据传送的数量。因此在确定与使用数据校验码的时候,必须考虑在不过多增加硬件开销的情况下,尽可能发现或改正更多的错误。常用的数据校验码有奇偶校验码、海明校验码和循环冗余校验码
奇偶校验码PCC
奇偶校验码是一种最简单、最常用的校验码。奇偶校验码广泛用于主存的读写校验或 ASCII码字符传送过程中的检查。
奇偶校验码的最小码距是2
组成奇偶校验码的基本方法是:在n位有效信息位上增加一个二进制位作为校验位P,构成n+1位的奇偶校验码。校验位P的位置可以在有效信息位的最高位之前,也可以在有效信息位的最低位之后。奇偶校验码可分为奇校验和偶校验
奇校验(Odd):使n+1位的奇偶校验码中1的个数为奇数
偶校验(Even):使n+1位的奇偶校验码中1的个数为偶数
采用奇偶校验的编码在传输过程中需要进行奇偶校验,以判断信息传输是否出错,如果接收方接收到一奇校验码中1的个数为偶数,或接收到一偶校验码中1的个数为奇数,则表示接收到的编码中有一位出错
奇偶校验码只能发现一位或奇数位个错误,而无法现偶数位个错误,而且即使发现奇数位个错误也无法确定出错的位置,因而无法自动纠正错误。由于现代计算机可靠性比较高,出错概率很低,而出错时只有一位出错的概率比多位出错的概率高得多,因此用奇偶校验检测一位出错,能够满足一般可靠性的要求。在CPU与主存的信息传送过程中,奇偶校验被广泛应用。
海明校验码
如前所述,合理地增加校验位、增大码距,能够提高校验码发现错误的能力。因此如果在奇偶校验的基础上,增加校验位的位数,构成多组奇偶校验,就能够发现更多位的错误并可自动纠正错误。这就是海明校验码的实质所在。
海明校验码是 Richard Hamming 于1950年提出来的。它的实现原理是:在数据编码中加入几个校验位,并把数据的每一个二进制位分配在几个奇偶校验组中。当某一位出错后,就会引起有关的几个校验组的值发生变化,这样不但可以发现出错,还能指出是哪一位出错,为自动纠错提供了依据。那么海明校验码究竟应该设置多少个校验位呢?
设有效信息位的位数为n,校验位的位数为k,则组成的海明校验码共长n+k位校验时,需进行k组奇偶校验,将每组的奇偶校验结果组合,可以组成一个k位的二进制数,共能够表示2种状态。在这些状态中,必有一个状态表示所有奇偶校验都是正确的,用于判定所有信息均正确无误,剩下的(2^k-1)种状态可以用来判定出错代码的位置。因为海明校验码共长n+k位,所以校验位的位数k与有效信息位的位数n应满足关系:2^k-1≥n+k
如果出错代码的位置能够确定,将出错位的内容取反,就能够自动纠正错误,因此,满足上式的海明校验码能够检测出一位错误并且能自动纠正一位错误。
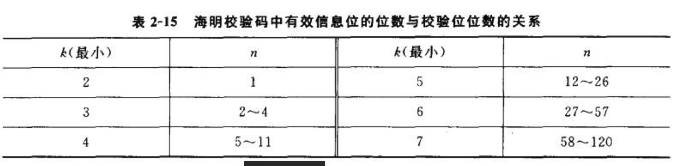



扩展的海明校验码的编码方式是:在检一纠一错的海明校验码的基础上,增加一个校验位P0,构成长度为n+k+1的编码。P0的取值是使长度为n+k+1的编码中1的个数为偶数(偶校验)或奇数(奇校验)
循环冗余校验码CRC
目前在磁介质存储器与主机之间的信息传输、计算机之间的通信以及网络通信等采用串行传送方式的领域中,广泛采用循环冗余校验码( Cyclic Redundancy Check,CRC)。循环冗余校验码是在n位有效信息位后拼接k位校验位构成的,它通过除法运算来建立有效信息和校验位之间的约定关系,是一种具有很强检错纠错能力的校验码。
CRC的编码思想

模2运算

CRC码的编码方法

CRC码的校验
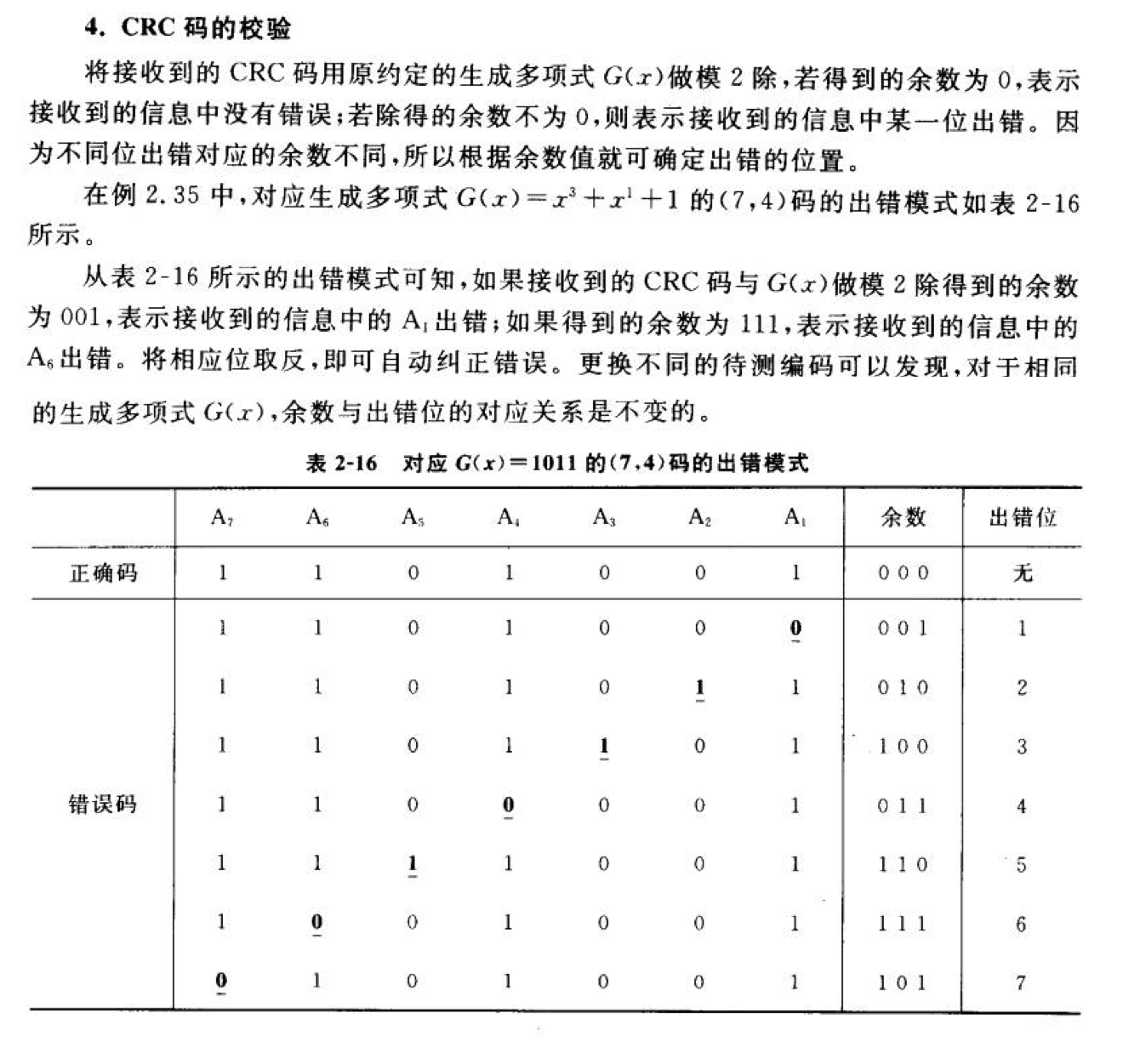
多项式
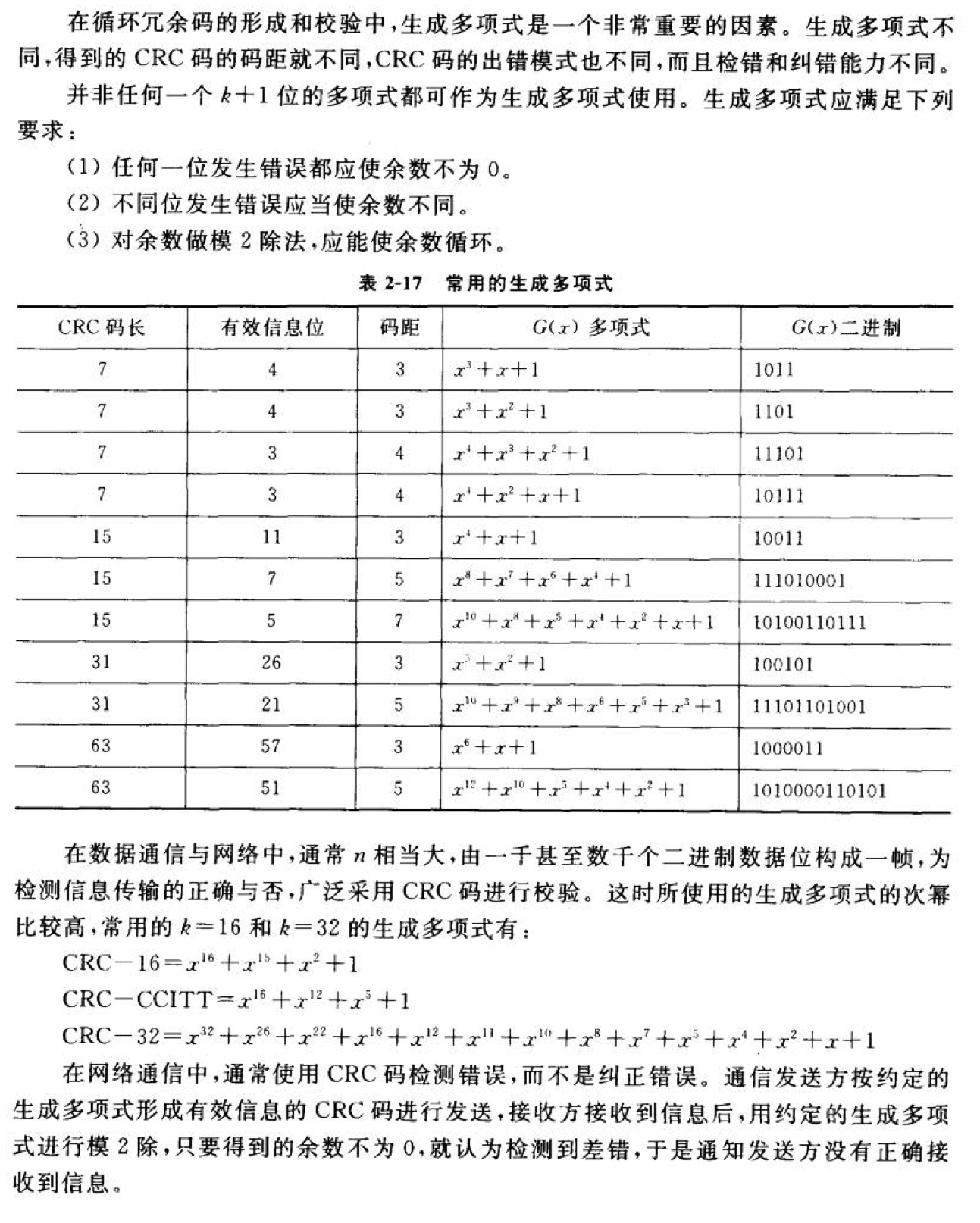
参考:
- wiki-错误检测与纠正
- 《计算机组成原理》,张功萱,P53-P65
- 《计算机组成原理》,唐朔飞,P100
- 最通俗的CRC校验原理剖析